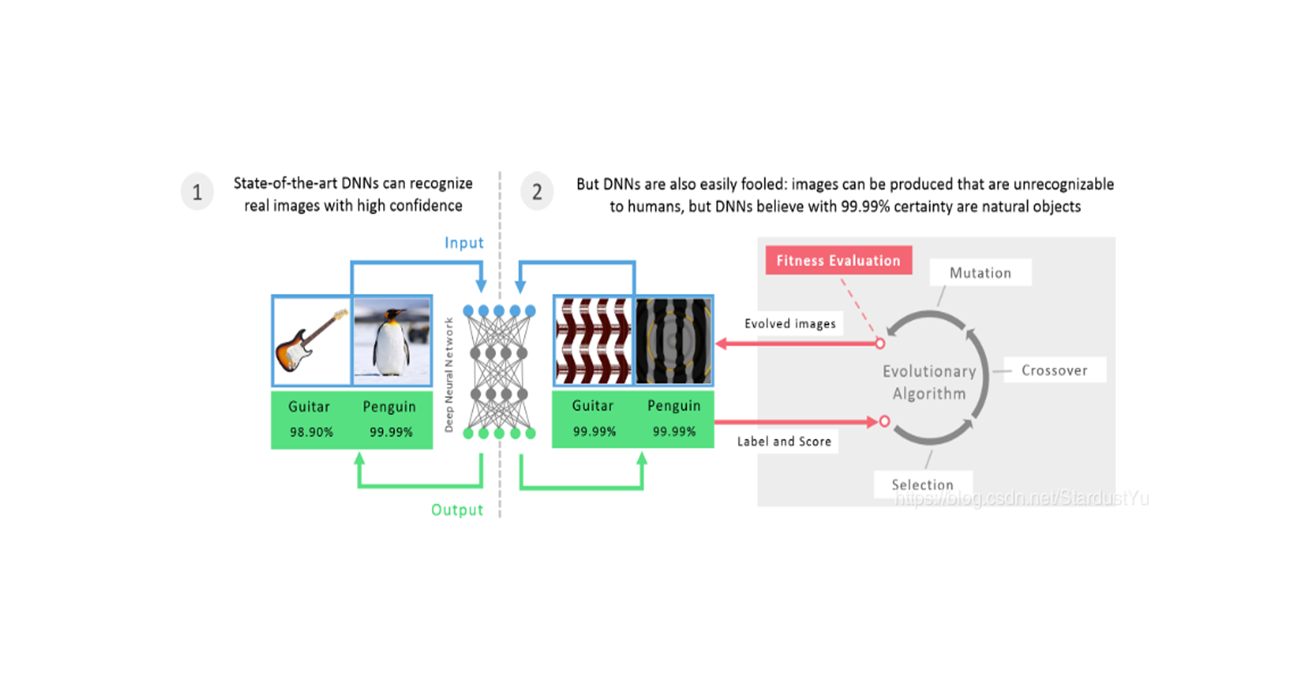
一、论文相关信息
1.论文题目
Universal adversarial perturbations
2.论文时间
2016年
3.论文文献
https://arxiv.org/abs/1610.08401
二、论文背景及简介
我们证明了存在一个通用的对抗扰动,可以造成大量的图片以很高的置信度被误分类。我们提出了一个系统的方法用来计算universal扰动,表明了SOTA的深度网络模型对这些扰动也是脆弱的。从经验角度对这些universal扰动进行了分析,发现这些扰动的泛化性很好。universal扰动的存在揭示了分类器高维决策边界之间的重要几何相关性。这也进一步表明了在输入空间中存在单个方向的潜在安全漏洞,攻击者可以利用这些方向来破坏大多数的分类器。
三、论文内容总结
- 提出了一种新奇的对抗样本种类,universal扰动,一个扰动可以用于整个数据集上来生成对抗样本。
- 提出了一种生成universal扰动的方法,利用Deepfool的优化手段,其可以对神经网络进行攻击
- 证明了universal扰动对新的图像和其他的模型都具有泛化性
- 可视化了universal扰动所带来的影响,发现了分类空间的一些信息,即:存在几个主要的类占据着大的分类空间。而universal扰动就是让图像去误分类成这些主要的类
- 通过对分类器的决策边界的几何相关性的解释,解释了universal扰动的泛化性。
附:如需继续学习对抗样本其他内容,请查阅对抗样本学习目录
四、论文主要内容
1. Introduction
我们能否找到一个小的扰动,能够fool一个SOTA模型的全部的数据集呢?在这篇文章中就证明了这样的一个扰动向量的存在性。这样的扰动被称为universal扰动。以下为示例:

universal扰动的存在,进一步揭示了深部神经网络决策边界拓扑的新见解。这篇论文的主要贡献如下:
- 确定了对SOTA模型的universal扰动的存在性
- 提出了一个计算universal扰动的算法,该算法寻找一组训练点的普遍扰动,并通过聚合发送连续数据点的原子扰动向量来进行
- 证明了universal扰动具有非常显著的泛化特性,因为由一组非常少的训练点计算得到的扰动能够fool其他的图片。
- 证明了这些扰动不仅在images之间是universal的,而且在模型之间也具有泛化性。
通过检验决策边界不同部分之间的几何相关性来解释和分析深神经网络对普遍扰动的高脆弱性
在这篇论文之前,也有大量的论文对对抗扰动的研究,比如通过优化问题或者梯度下降来找到对抗扰动,但是,这些方法得到的每一个对抗扰动仅仅依赖于一个数据点,也就是说,他们在数据点这个方面是独立的。但是,将对抗扰动应用到一个新的图片时,要解决的正式数据之间的独立性问题,这需要使用分类器的全部的知识。而universal扰动则避免了这个问题。
2. Universal perturbation
记$ \mu$ 表示$ \mathbb{R}^d$ 的图像分布,$ \hat{k}$ 表示一个分类器,$ x \in \mathbb{R}^d$ ,其标签为$ \hat{k}(x)$ 。我们的目标就是找到一个扰动向量$ v \in \mathbb{R}^d$ ,能够对分布为$ \mu$ 上的大多数数据进行攻击,即,找到一个向量$ v$ ,使得:
我们将重点放在分布为$ \mu$ 的数据集的情况下,其包含了大量的变量。在这种情况下,我们证明了小的universal扰动的存在,其基于$ l_p,p\in[1,\infty]$ norm,目标变成了,找到一个向量$ v$ 满足下面两个条件:
参数$ \xi$ 控制了扰动的大小,$ \delta$ 量化了对以分布$ \mu$ 采样的全部是图片,攻击所期望的fooling rate。
令$ X = {x_1,…,x_m}$ 表示一组分布为$ \mu$ 的数据集。算法通过迭代的方式对$ X$ 上的数据点进行处理,逐渐的构建出一个universal扰动。在每次迭代过程中,我们都会找到一个最小的扰动$ \Delta v_i$ ,能够把当前的样本点$ x_i + v$ 往$ x_i$ 的决策边界移动,然后把$ v_i$ 汇总到总扰动中。更详细的说,就是,如果当前的$ v$ 不足以欺骗样本点$ x_i$ ,那么我们就找到一个新的额外的扰动$ \Delta v_i$ ,其能够欺骗样本点$ x_i$ 。$ \Delta v_i$ 的优化问题为:
其过程大致如下:

为了保证限制条件$ ||v||_p \le \xi$ 的成立,即更新后的扰动会被投影到$ l_p$ 的球形空间(半径为$ \xi$ ,中点为0)中去,定义一个映射算子$ P_{p,\xi}$ :
所以,我们将新的得到的扰动$ \Delta v_i$ 汇总到$ v$ 时,采用$ v = P_{p,\xi}(v+\Delta v_i)$ 。
当我们在数据集$ X$ 上的扰动成功率大于一定程度后,就停止迭代过程,即:
其算法过程如下:

有趣的是,在实际过程中,$ X$ 上的样本点数目并不需要特别大,就能够计算得到一个能够对$ \mu$ 分布上的图片都进行攻击的universal扰动。
值得注意的是,上面的算法在神经网络这样的大模型中并不会收敛,作者采用了一些有效率的估计方法(来自论文Deepfool)来解决这个问题。指的注意的是,上面的算法并不是去寻找一个最小的扰动,而是去找到一个能够使得$ l_p$ 最小的扰动。而且当$ X$ 不同时,其得到的$ v$ 也会不一致。
3. Universal pertubations for deep nets
A. 神经网络对Universal扰动的鲁棒性
我们基于ILSVRC 2012数据集(验证集有50000张图片),对不同的神经网络进行了评估,记录攻击成功率。采用了两组参数,一组$ p=2,\xi=2000$ ,另一组$ p = \infty,\xi=10$ 。

其中$ X $ 是来自训练集的10000张图片,平均每个类别10张。
$ X$ 数据集的样本数的不同,所得到的结果也不同,当$ X$ 仅包含500张图片是,其可以实现30%的攻击率,这对ImageNet是很重要的,这表明,我们可以仅仅使用一点点的图片,即使不包含所有的类被,就可以欺骗大量的未知的图片。这也表明该算法在未知的数据上具有显著的泛化性

B. Cross-model universality 模型间的泛化性
上一届,证明了universal扰动在数据上具有泛化性,在这一节,证明universal扰动在模型之间具有泛化性。我们使用一个模型(比如VGG-19)生成扰动,然后在另一个模型(比如GoogLeNet)上进行验证。于是,我们在六个不同的模型上进行交叉验证,记录其攻击成功率。

其中行表示的是生成扰动的模型。
可以看到,对应于一些模型来说,其生成的扰动的泛化性很好,比如VGG-19生成的扰动。
这表明,我们的universal扰动在一定程度上可以泛化到不同的模型上。
C. Visualization of the effect of universal pertubations 可视化Universal扰动的影响
为了得到universal扰动对图片带来的影响,我们首先可视化了ImageNet的验证集上label的分布。我们构建了一个有向图$ G=(V,E)$ ,节点表示label,有向边$ e=(i \to j)$ 表示类别$ i$ 的图像大部分都能被universal扰动误分类为标签$ j$ ,也表明标签$ i$ 被fool时,首选标签是$ j$ 。
作者对GoogLeNet的扰动进行了可视化处理,展现出了一种奇特的拓扑结构。奇怪的地方在于,这个有向图是由多个不相交的组件并起来的,每个组件的所有边都连接到一个目标标签上,如:

通过这个可视化,清晰的展示了存在几个主要的标签,universal扰动主要是让原始图像被误分类成这几个主要标签。我们假设这些主要的标签占据了图像空间中的大部分区域,因此代表了fool这些原始图像时的好的候补标签。注意,这些主要标签可以自动的被我们的算法识别。
D. Fine-tuning with universal pertubations
这一节是评估用universal扰动来进行fine-tuning时带来的影响。
作者使用了VGG-F结构,然后用universal扰动修正数据集,然后对网络进行fine-tuning。注意:在修正数据集时,每个样本都有50%的概率加上universal扰动或者不变。而且,为了增加universal扰动的多样性,作者预计算了10个不同的universal扰动,然后随机的选择一个以50%的概率加到样本上。
网络经过了5轮fine-tuning的迭代,为了评估fine-tuning对网络鲁棒性的影响,作者对fine-tuning后的网络计算得到了新的universal扰动,使用的参数为$ p=\infty,\xi=10$ ,然后记录其攻击成功率。发现,经过5轮迭代后,其成功率只有76.2%(相比于之前的93.7%)。
尽管fine-tuning带来的提升很大,但对universal扰动仍然是脆弱的。作者对上面的操作进行了重复操作,发现重复操作后,其成功率有80%。也就是说,重复的fine-tuning并不一定生效。
4. Explaining the vulnerability to universal perturbations
这一节的目标就是来分析和解释深度神经网络对universal扰动的脆弱性。
为了了解universal扰动的特性,我们首先将其与其它类型的扰动进行了对比,这些扰动有:1、random扰动;2、利用随机采样(DF和FGSM方法)得到的对抗扰动;3、在$ X$ 上的对抗扰动和;4、images的均值。对每一个扰动,我们都绘制了相变图,展示了在验证集上的攻击成功率对$ l_2$ norm大小的变化,通过用乘法因子相应地缩放每个扰动以具有目标范数来实现不同的扰动范数。

universal扰动与随机扰动的巨大差异表明,universal扰动利用了不同决策边界间的几何相关性。事实上,如果不同数据点附近决策边界的方向完全不相关(并且与决策边界的距离无关),则最优的universal扰动的范数将与随机扰动相差无几。
之后就是对分类空间的几何相关性的解释。
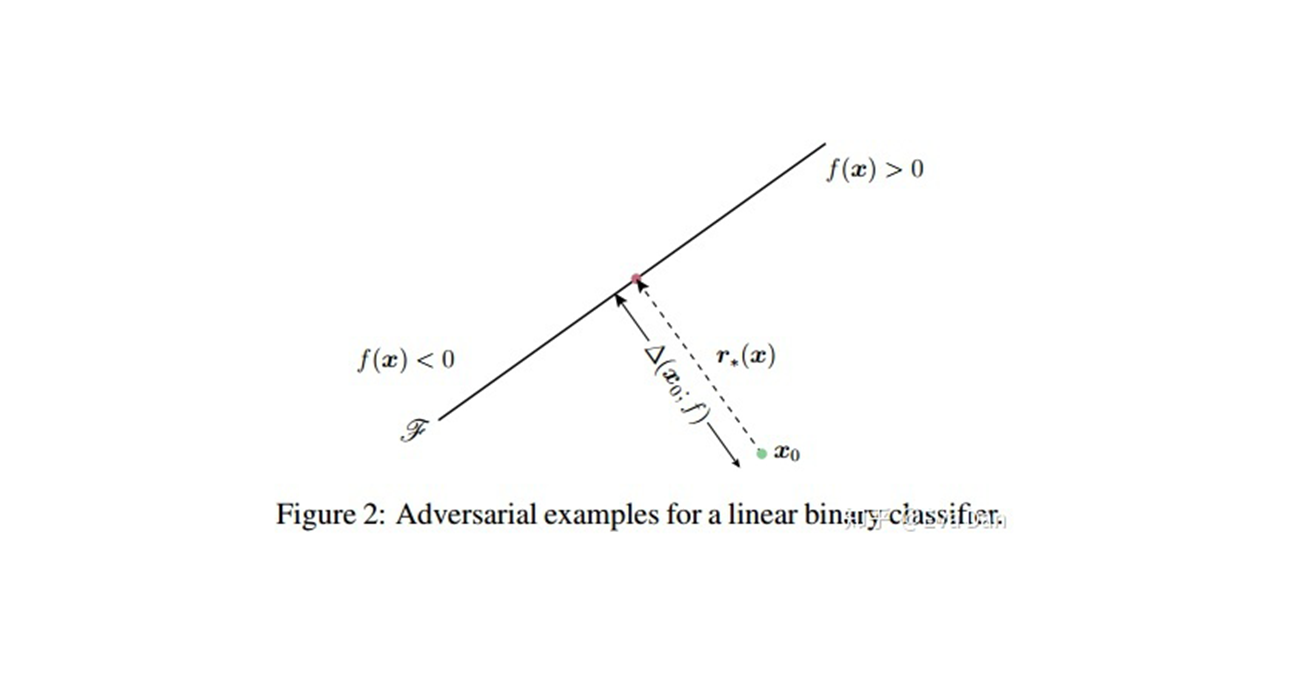
对于验证集的每一个图片$ x$ ,我们都会计算他的对抗扰动向量$ r(x) = arg min_r||r||_2 s.t. \hat{k}(x+r)\ne\hat{k}(x)$ 。易知,$ r(x)$ 就是数据点$ x$ 到决策边界的法向量,所以$ r(x)$ 也就表示数据点$ x$ 附近区域的决策边界的几何特性,为了量化整个分类器的决策边界的几何特性,我们可以计算这样一个矩阵:
矩阵$ N$ 是由$ n$ 个数据点的法向量组成。
对于二分类的线性分类器来说,$ N$ 的秩为1,因为所有的法向量都可以被线性表示。
为了去了解复杂分类器的决策边界的相关性,我们去计算$ N$ 的奇异值。其中,我们使用CaffeNet结构来计算$ N$ 。在这样的配置下,我们将会展示由n列从单位球面均匀采样的点$ x$ 获得的矩阵$ N$ 的奇异值。当我们慢慢地减少采样点n值时,发现矩阵$ N$ 的奇异值减少的更快,这也证明了,深度网络的决策边界存在巨大的相关性和冗余。更精确的是,这表明存在一个子空间$ S$ ,其维度$ d’$ 远小于原本的空间维度$ d(d’ \ll d)$ ,该子空间包含着大部分的法向量。我们假设universal扰动的存在是因为存在这样一个低维的子空间,能够捕获到不同的决策区域边界的相关性。实际上,这样的子空间聚集了不同区域的决策边界的法向量,属于这个子空间的扰动也就能够愚弄大部分的数据点。
为了验证这样一个假设,我们从子空间$ S$ 中随机选择一个向量,这个向量由前100个特征向量组成,设置其norm最大值为2000,计算他在不同的数据上的攻击成功率,这有点奇异值分解SVD的意思。经过实验得到,这样的扰动向量能够攻击接近38%的图像。而且,在子空间$ S$ 的一个随机的向量,比一个随机的扰动,攻击表现得好,因为在norm最大为2000时,随机扰动得成功率只有10%。
同时,这样的一个低维子空间解释了universal扰动得泛化特性。
5. Conclusions
作者证明了universal扰动的存在,提出了一个方法来生成universal扰动,同时阐明了universal扰动的几个特性。同时发现,universal扰动能够在不同的分类器之间泛化的很好。同时我们进一步解释了这种扰动的存在与决策边界的不同区域之间的相关性之间的关系,这让我们了解到了神经网络的决策边界的几何性,也让我们对其有了更好的理解。在决策边界不同部分的几何相关性的理论分析将会是未来研究的一部分。